 Modern science takes for granted that the naturalistic origin of life, called “abiogenesis” or “chemical evolution” or “pre-biotic evolution” is extremely improbable but not impossible. “Life” here means a single self-reproducing and self-sustaining biological cell. Science claims that life can arise from inorganic matter through natural processes. This unsupported claim is based on the conviction that all arrangements of atoms are possible and life is considered merely one such arrangement. In what follows I try to explain that such a believe is unfounded because abiogenesis is impossible in principle. My argument, expressed in its simplest form, has two main steps: (1) to show that a computer cannot be generated naturalistically; (2) to show that biological systems contain computers. From #1 and #2 I will argue the impossibility of abiogenesis.
Modern science takes for granted that the naturalistic origin of life, called “abiogenesis” or “chemical evolution” or “pre-biotic evolution” is extremely improbable but not impossible. “Life” here means a single self-reproducing and self-sustaining biological cell. Science claims that life can arise from inorganic matter through natural processes. This unsupported claim is based on the conviction that all arrangements of atoms are possible and life is considered merely one such arrangement. In what follows I try to explain that such a believe is unfounded because abiogenesis is impossible in principle. My argument, expressed in its simplest form, has two main steps: (1) to show that a computer cannot be generated naturalistically; (2) to show that biological systems contain computers. From #1 and #2 I will argue the impossibility of abiogenesis.
First off, some principles and definitions.
Principle 01: Nothing comes from nothing or “ex nihilo nihil”.
Principle 02: “Of causality”, if an effect E entirely comes from a cause C any thing x belonging or referenced to E has a causative counterpart in C. In fact if something x of E hadn’t a counterpart in C, x would come from nothing and this is impossible due to the ex-nihilo-nihil principle. It may help to think about causation of E by C as a mathematical function where every ‘e’ of E is image of some ‘c’ of C.
Definition 01: “Symbol”, a thing referencing something else. Examples: (1) a circle drawn on a piece of paper may symbolize the sun; (2) the chemical symbol CGU (the molecular sequence cytosine / guanine / uracil) references arginine amino acid in the genomic language; (3) the word “horse” symbolizes the “Equus ferus caballus”. The choice of a symbol for a thing is purely contingent and arbitrary. No natural law forces such choices. A symbol is an indirect way to point to something, whereas physical objects are always direct in their action.
Imagine a photon on a collision trajectory with an arginine molecule. On the fly the photon cannot decide: “I prefer to hit the arginine molecule indirectly, I hit CGU instead – which has a symbolic-mapping with arginine – and in turn something else will hit the arginine for me”. The photon must obey quantum mechanics laws that do not contain the symbol CGU=>arginine, given that it is entirely arbitrary. As a consequence the photon must hit the arginine molecule directly, without passing through symbolic links that transcend its laws. This is true for all physical objects and their laws.
Definition 02: “Symbolic processing” is a process implying choices of symbols and operations on them. The basic rules of symbolic processing are contingent and arbitrary and as such are not constrained by natural laws.
Definition 03: “Language”, mapping between sets of abstractions and sets of material entities by mean of symbolic processing.
Definition 04: “Instruction”, operational functional prescription on data and their behaviour by means of a language. Software consists of sets of instructions usually deployed to a target computer system (hardware) to be run. Instructions are something qualitatively different from arrangements of objects and can never be totally reduced to them.
To illustrate, let me command “put the apples on the table”. My instruction is qualitatively different from apples. Materially my command will produce the effects: (1) Moving the apples as a process and (2) An arrangement of apples as a final result. Nevertheless the instruction, as cause, is different from apples. Indeed because an instruction governs arrangements it is not simply an arrangement. This is the fundamental ontological difference between an abstract principle overarching material objects that obey it. An instruction, to be effective in an information processing system must be coded by means of a language and deployed to a target system for its execution. Language makes a material arrangement become a symbol of an abstract instruction. My put_the_apples_on_the_table instruction was coded in the English language because it was intended for humans. However it could be coded in many other ways depending on the system that must run it. For example in digital computers the programmer’s high-level instructions are coded finally in machine code, arrangements composed of 1s and 0s, represented by physical states of the hardware.
Let’s continue with our apple analogy. Let’s imagine that chance and necessity could actually build an apple-dispenser system which is able to function by reading instructions. We would like it to execute the instruction put_the_apples_on_the_table. Since the Chance and Necessity system (C&N) doesn’t understand English and deals only with apples, we might codify the instruction as a binary string, e.g. according to the ASCII code or whatever, where 1 is an apple and 0 is no apple. In other words we are using arrangements of real apples to code instructions on how to distribute apples. Our message is written in “apple code”. Thus material apples symbolize an abstract instruction. Let’s input this string into the C&N system and see what happens. When this arrangement is processed, we find that the C&N system unfortunately cannot distinguish between a generic set of apples to distribute and the codified apple string to be read and executed. How could C&N be able to distinguish between them if symbols simply don’t exist for C&N? So our C&N system doesn’t work. It has an irresolvable semantic/syntactic problem for C&N. The C&N lacks the capability to chose between apples “to eat” and apples “to read”, so to speak. The machine eats the apples instead of reading them. It cannot be a software-driven machine.
Definition 05: Turing Machine (TM), abstract formalism composed of a finite state machine (FSM) (containing a table of instructions) + devices able to read / write symbols of an alphabet on one or more tapes (memories). A Turing Machine is the archetype of computation based on instructions. It is what we understand as a computer. Its main parts form what Michael Behe calls an “irreducibly complex system” [1]. Note that computation overlaps – as a higher abstract layer – a lower layer of things that per se are not computable, e.g. the choice of using an alphabet, the choice of its symbols, and the choice of the language and its rules are purely contingent and arbitrary. They don’t come from a mechanical procedure because they are free choices. Hence computation (which by definition is mechanical and never free) presupposes and works only thanks to a substrate which is fundamentally incomputable.
Definition 05a: “Halting problem”. Any specialized TM, given an input, may finish running (halt) or continue to run forever (infinite loop). If it halts, the TM has computed the input. Otherwise if it runs forever the input is not computed. Thus the problem in computability theory was to determine if there could be a super TM such that – given the description of a specialized TM – it would determine whether or not it would halt on a particular input (i.e. compute it in a finite number of steps). However, Turing proved that such a super TM general enough to be able to decide the halting for any specialized TM cannot in principle exist. The halting problem is incomputable.
Definition 06: “Physical computer”, a physical implementation of an abstract formalism of computation. It can be mechanical, electronic, chemical. It is an arrangement of atoms (hardware) that works out a computation.
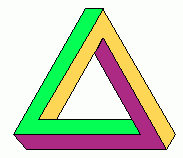
Principle 03: Formalism > Physicality (F > P) [2], formalism overarches physicality, has existence in reality and determines its physical implementations. A consequence is that implementation has limits directly related to and implied by formalism. Another consequence is that not all atom arrangements are possible. Atom arrangements against the natural laws, logic and mathematics are impossible. Here are three examples: (1) a perpetual motion machine is an impossible arrangement because it contradicts the formalism of thermodynamic laws; (2) a TM computing the “halting problem” (see Definition 05a) is an impossible arrangement due to the formalism of computability theory; (3) the Penrose (or tribar) triangle -though it can be drawn on a 2D surface – is an impossible arrangement in 3D because it doesn’t meet the constraints of the formalism of Euclidean geometry of the 3D space. See figure at the top.
The key point is that the impossibility of certain formalisms implies the impossibility of the related physical implementations. Abstractness matters. It drives matter.
According to modern science the universe can be considered a system that computes events according to the physical laws. According to Gregory Chaitin “the world is a giant computer”, “a scientific theory is a computer program that calculates the observations” [3]. This formulation allows us to frame the physical sciences in the very general paradigm of information sciences:
inputs => processor => outputs
This leads to the following:
Definition 07: “Primordial soup” or “naturalistic scenario”, an imagined physical implementation of a computer which can compute inputs of atoms/energy into output of arrangements of atoms. The instructions of such a computer are the natural laws, which somehow function as the “software” of the cosmos. This proposed system is synonymous with the “chance & necessity” (C&N) scenario:
atoms/energy => [ C&N ] => atom arrangements
One can think that for each of the n atoms in input a function must be computed:
f(a1,x1a,y1a,z1a,…) = (x1b, y1b, z1b,…)
where on the left we have all the characteristics / arguments of the situation related to the atom a1 when it is in the initial location A (coordinates, etc.) and on the right we have all the characteristics related to the atom a1 when it moves to the final location B.
This model is very general and is based on the concept of instruction = law because all agree that there exist natural laws computing events and processes.
Definition 08: “Constructor”, an information processing device that constructs a system from parts by means of internal coded instructions.
parts => [ constructor ] => system
It is similar to what John von Neumann [4] called a “universal constructor ” and which, together with a controller, a duplicator and a symbolic description of the machine, are the necessary component of a self-replicating automaton. Cells are living examples of self-replicating automata. A cybernetic constructor must necessarily contain a computer within itself.
Definition 09: “GRC” (genome / ribosome / genomic code) is a chemical implementation of a constructor, which makes proteins from amino acids according to the genomic language and instructions. It is a fundamental system in the molecular machinery of any biological cell, whose kernel can be modeled as a multi-tape TM.
amino acids => [ GRC ] => proteins
The DNA-polymerase molecular machine produces RNA from DNA (genome). In turn the ribosome molecular machines translate messenger RNA (mRNA) and builds polypeptide chains (proteins) using amino acids carried by transfer RNA (tRNA). DNA – a couple of complementary strands of molecules composed of four symbols {A, T, G, C} which can be written and read according to the “genetic code” – may be thought of as a tape of a TM.
Leonard Adleman, another mathematician, who is the pioneer of the so-called “DNA computing”, in his first groundbreaking work [5], recognised that “biology and informatics, life and computers are tied toghether”, and said that “it’s hard to imagine something more similar to a TM than the DNA-polymerase”. The DNA-polymerase is an important enzyme of the cell that is able, starting from a DNA strand, to produce another complementary DNA strand. (Complementarism means that C changes to G and T changes to A.) This nanomachine slides along the filament of the original DNA reading its bases and at the same time writes the complementary filament. As a TM begins an elaboration from a starting instruction on the tape likewise the DNA-polymerase needs a start mark telling it where to begin producing the complementary copy. Normally this mark consists of a DNA segment called a “primer”.
In some senses biological computers are more advanced than artificial ones. First the DNA language and the genetic code are highly optimized. Moreover the memory is used more efficiently. In fact, according to many researchers, often the same sequence of DNA contains multiple information (e.g. codifies for proteins and at the same time stores data related to other cellular processes or structures). Biological technology is superior because in multiple-coding DNA we derive many different levels of interpretation from the same span of code, an astounding compression of data so inconceivably difficult it has never even been attempted in human technology. It is clear that the problem of reading from memory in these cases of multiple interpretations becomes ever more unreachable by C&N.
Thesis 01: From a primordial soup of disorganized atoms as input a cybernetic constructor as output cannot spontaneously arise.
As said, a constructor implies a physical implementation of a computer formalism. In a naturalistic scenario, if the constructor formalism doesn’t exist already in the input, it should be generated by the C&N computer (for the principle of causality and the principle of existence of formalism, F > P). But we saw that this formalism doesn’t come from a computation. Then C&N cannot create it. That is expressed in the jargon of informatics by the GIGO principle (“Garbage In, Garbage Out”).
In the naturalistic scenario we are given to understand that formalism appears spontaneously in the output of a C&N computer. The principle of causality tells us that either C&N or intelligent input must have created the formalism. Yet we have already determined that a C&N computer cannot create a computer formalism. Therefore, if such formalism is present in the output of C&N, it must necessarily have first been introduced via input into the computer. There is no other option. But in the naturalistic scenario the input is limited to disordered atoms, which have no formalism. Therefore, given that intelligent input is prohibited and C&N is incompetent, no computer formalism can arise in the output of a C&N computer. The naturalistic scenario cannot produce the wonders demanded of it.
By the way, a computer formalism contains what David Abel calls “prescriptive functional information” (PI) [2] that is of course a form of what William Dembski calls “complex specified information” [6] and justifies what Michael Polanyi said: “the information content of a biological whole exceeds that of the sum of its parts” [7]. If this formalism x doesn’t exist, the output would have an information content equal to the sum of its atoms and nobody denies that a biological system is something more than a container of disordered atoms or a tank filled with gas molecules. That “formalism precedes physicalism” is expressed by another researcher this way:
“That a semantic does exist, i.e. that the information stored in the DNA is carrier of meaning, is inferable from the fact that biological systems do work, the information is translated in a sensible manner in functioning biological processes” [8].
Of course a physical computer can exist when it is designed and constructed by intelligence.
In the following I will answer some typical objections.
Obiection 01: “The constructor formalism in output doesn’t exist. It is only in your mind. In output there are atoms only. As such the formalism cannot have inhibitory power on atoms because what doesn’t exist cannot inhibit. Therefore the constructor arrangement might be the output by a natural C&N computer”.
Answer 01: This objection is a negation of the F > P principle. Formalisms exist and govern matter. If formalisms existed only in our minds they would have no causative power. In no way could they influence matter. But they do interact and influence. Our three examples of impossibility – perpetual motion machines, TMs computing the halting problem and three-dimensional Penrose triangles – cannot be produced as real arrangements of atoms. Their existence is denied by nothing but certain formalisms. Formalisms have inhibitory power on atoms.
Obiection 02: “Given enough time a computer implementing a random generator of characters can generate Shakespeare’s Hamlet; therefore, a computer can create symbols and language”.
Answer 02: Such static pseudo-symbols are not a functioning formalism. This case is entirely different from generating a dynamic functional hardware / software system as a cybernetic constructor, which makes a constructive job in the physical space-time. To claim that C&N can create coded instructions able to be executed is as absurd as saying that natural forces, by moving apples and tables, can add to the set of natural laws an additional put_the_apples_on_the_table law.
Obiection 03: “The genetic code in a GRC constructor could have arisen from a shorter alphabet, this one from a shorter one and so on, by incremental steps”.
Answer 03: This process in no way could reduce the overall prescriptive information in the code. As Don Johnson says
“we have examined both the functional (especially prescriptive) information and the Shannon complexity of life, with Shannon information placing limits on information transfer, including the channel capacity limit that requires an initial alphabet of life to be at least as complex as the current DNA codon alphabet” [9].
Obiection 04: “The natural laws can calculate the coordinates of a real physical computer and this suffices to prove that natural laws can create computers”.
Answer 04: No. This doesn’t suffice to prove that they can do that. The Penrose triangle cited above (example #3 of impossibility) offers us a useful analogy. The Penrose triangle can be drawn in 2D but not constructed in 3D. In other words, the coordinates of the 2D drawing can be computed while the coordinates of the 3D construction cannot be computed. What difference exists between a 2D Penrose triangle and a 3D one? The 3D object has an additional dimension in respect to the 2D figure. This additional dimension cannot be computed. The problem of creation of a computer by natural laws is analogous. The natural laws could calculate by chance the coordinates of a real physical computer (as the objection says) but cannot calculate its “additional dimension” of computer formalism. Since a computer is coordinates + formalism the natural laws should calculate both (and they cannot), just as a 3D Penrose triangle should be calculated in all its three dimensions x, y, z yet it cannot. To claim that the natural laws calculate the coordinates of the computer (as the objection claims) is similar to obtaining a 3D Penrose triangle by calculating the x and y coordinates but omitting the z coordinate. Just as in a 3D Penrose triangle the z coordinate must be computed so a computer formalism produced by C&N should be computed by natural laws but is not as thesis 01 states. As the two-dimensional drawing of a Penrose triangle is a representation of an impossible three-dimensional body, likewise it is an illusion that C&N can calculate a true computer.
Obiection 05: “In your apple analogy C&N could create a mechanism that distinguishes between generic arrangements and codified arrangements and read the latter”.
Answer 05: I state that C&N doesn’t write/read (symbolic processing) to prove that it cannot create a constructor (containing a computer). A mechanism able to distinguish between apples “to eat” and apples “to read” would have the cybernetic structure of a constructor, so the objection is circular because it presupposes that C&N creates a computer just from the beginning. But that C&N creates a computer is exactly what has to be proved in the first place.
Thesis 01 has an important and direct application in the biological field about abiogenesis for the following:
Corollary 01: Given that any biological cell contains GRCs, given that a GRC is a constructor, and given that a constructor doesn’t arise from a naturalistic scenario, the naturalistic origin of life is conceptually impossible. So far this corollary has not been not falsified by experiment. In fact in the Urey-Miller experiments only some of the amino acids formed. But amino acids are simple arrangements of atoms, not machines, not TMs, not constructors. More significantly, no GRCs formed.
“Pasteur’s claim that any living being comes from another living being (‘omne vivum ex vivo’) continues to fully agree with all experimental data of pre-biotic chemistry” [7].
Against this argument from impossibility, it doesn’t help to resort to phantasmic multi universes or infinite time, as some do. An impossible thing remains such also in infinite universes. 2+2=5 continues to be untrue in infinite universes. Again as Abel says:
“Imagining multiple physical universes or infinite time does not solve the problem of the origin of formal (non physical) biocybernetics and biosemiosis using a linear digital representational symbol system […] physicodynamics cannot practice formalisms” [2].
If biological cells contain computers and computers cannot be created by C&N, then the origin of such biological systems is not natural and implies the intervention of that which is able to work out symbolic linguistic information processing namely, intelligence. Such transcendent intelligence, whose hardware and software designs are before our eyes, may be called the Great Designer.
References
[1] Michael Behe, “Darwin’s Black Box”, 2003.
[2] David Abel, “The First Gene”, 2011.
[3] Gregory Chaitin, “Leibniz, Information, Math and Physics”, 2004.
[4] John von Neumann, “Theory of self-reproducing automata”, 1966.
[5] Leonard Adleman, “Molecular computation of solutions to combinatorial problems”, 1994.
[6] William Dembski, “The Design Inference”, 1998.
[7] Michael Polany, http://www.iscid.org/encyclopedia/Michael_Polanyi
[8] Reinhard Junker, Siegfried Scherer, “Evolution – ein kritisches Lehrbuch”, 2006.
[9] Don Johnson, “Programming of Life”, 2010.