This problem has been resolved by a professor of mathematics. The solution is elegant. The contest is closed. I love the Internet! –WmAD
/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\
I’m offering the first person who completely resolves the following conjecture $1000 cash. I need a complete error-free proof and I need to be able to use it in my writings (of course, I’ll give full credit to the mathematician who proves it).
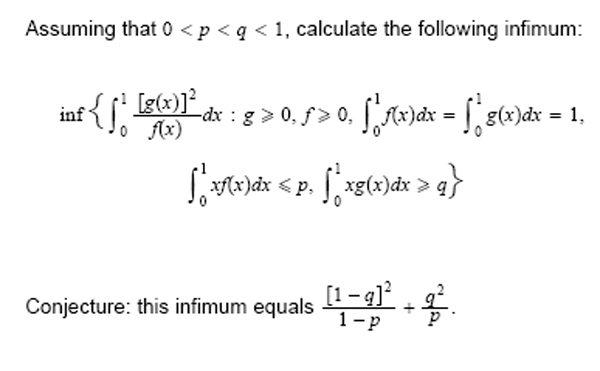
This conjecture is relevant to the conservation of information.