In a previous post (see here) I wrote: “necessary but not sufficient condition for a self-reproducing automaton is to be a computer”. Biological cells self-reproduce then for this reason work as computers. But “computer” is a very generic term (it means a device able to compute, calculate, process information, rules and instructions). Computer-science studies a series of models, of increasing complexity, which deserve the name of “computer”. It may be interesting to briefly analyze these models and discover which of them cells are more similar to. At the same time I hope my analysis will clear more what said in that post.
The series of computing architectures goes from the abstract state machines to the real computers and servers we use nowadays. The first basic model able to process instructions is the finite state machine (FSM). It is a controller that receives inputs and generates outputs assuming sequentially a finite set of different inner states. Many activities inside a cell are configurable (as first raw approximation) as FSM processes because they imply many different states while processing input and outputs. Inputs and outputs can be whatever thing or event (as a trigger signal to turn on a gene, the creation of a protein and so on). Different internal states may be related to, say, what genes are on and what are off at a given instant, or to different phases of the life of the cell, etc. The compilation for a given biological process of the complex transition table, composed of all quadruples {state N, input, state (N+1), output} implies a complete knowledge of that process at the molecular, chemical and physical level. Obviously all that doesn’t mean that cellular processing cannot be modeled by mean of other modeling languages. Since the complexity of the cell entails several concurrent activities carried-out by its many distributed sub-systems it could also be described better by the more powerful formalisms of the Petri nets suite, which were invented indeed to describe from chemical processes to any real-world process. But for what matters here we don’t need to enter this argument now, because also considering these different descriptive formalisms, the conclusions wouldn’t change.
The second abstract computing model is the specialized Turing machine (TM), which is a FSM (control unit) with the additional ability to read and write a memory. Alan Turing conceived the memory in the form of a tape but it could be whatever support able to store information. A version of his machine had two tapes, one for reading and the other for reading/writing, but conceptually and from the viewpoint of the computation power makes no difference. Each cell of the memory can contain a symbol (chosen from a finite alphabet of symbols). The memory hosts the inputs (considered front-loaded) and the outputs (which will be written by the FSM during the execution). The control unit contains the program that generates the outputs from the inputs. A TM can work-out only a specific task (that described in the program of its FSM).
Since a cell, beyond to work as a FSM, is able to read and write, can behave as a TM. In fact in a cell the DNA-RNA symbols (A, T, G, C, U) are the alphabet. DNA is the molecular “tape” that DNA and RNA polymerase machineries can read. Is DNA read-only or also writable? The so-called “central dogma” of molecular biology (implying that DNA is read-only) has been partially disproved recently by discovering some phenomena (non-coding RNA, reverse transcriptase, epigenetics, etc.). These findings show that in a sense DNA is also writeable, then information can flow both ways. However also if the DNA were non writable, there are many situations where the control unit of the cell writes data (e.g. RNA transcription, DNA duplication). Ideally we could concatenate all these output molecular sequences in a long strand and this way the cell seems more a two-tape TM.
The third computing model is the universal Turing machine (UTM). It is a more powerful TM with a FSM that, thank to some particular bootstrap instructions, can run any program stored in the memory. These programs are different instructions tables (a specialized TM contains only one table in its control unit and as such can run one task only). A real UTM can potentially work-out whatever algorithm (Church’s thesis). I say “potentially” because of course a UTM can work-out only the algorithms really installed in its memory. Its universality is potential. A cell cannot be considered properly a UTM because its memory may contain many different codes, each of them specifically dedicated to a different biological task, but it is unlikely it can run any algorithm. What the so called DNA-computing or “molecular programming” specialists are trying to do is to use the cellular machinery as a UTM to solve scientific problems that nothing have to do with biology, by modifying it and eventually resorting to some external manual operations in the lab.
The fourth computing model is the von Neumann machine. It is a stored-program registers-based UTM able to input and output from/to the external world. In particular a von Neumann universal self-replicator (see its description in the post referenced above) contains in its memory a particular program of self-replication and the output can be a copy of itself. We can say that a cell is similar to a von Neumann self-replicator but it is unlikely a cell is really a universal one because is not a UTM (see above) and it cannot replicate whatsoever thing. However cells can run external code: in fact they can replicate viruses, i.e. “alien” DNA instructions (not able to self-replicate by themselves) that parasitically infect a cell for being self-replicated. But the property of universality is a strong assumption and, so far as we know, cells haven’t such property.
~~
From the Intelligent Design point of view what matters is to know if a thing is designed. We could consider a TM and ask if it can arise by unguided evolution, that is by mean of a step-by-step incremental process driven only by chance and necessity. Whether we discover that just a TM cannot arise by evolution, then to greater reason, given that a cell is something more than a TM and self-reproduces, the design inference on cell will be straightforward.
Now let’s see why a TM cannot be the product of evolution. To describe dynamically a TM in a simple way we can think it as a machine that goes through a sequence of transitions (the transition table). Each of these transitions is composed of the following items: the state in which the TM is now, the symbol read, the symbol to be written (eventually no writing), the shift on the tape and the next state. Therefore to have a functioning TM we need a set composed of the following elements: (1) a transitions table; (2) an alphabet of symbols; (3) a tape to store symbols; (4) the ability of reading/writing; (5) the ability to move across the tape. It is easy to see that this set is irreducibly complex (IC). Without #1 the TM knows absolutely nothing about what to do. Without #2 the machine moves across the tape but there is nothing to read or write. Without #3 the machine tries to read and write but there is no tape. Without #4 the TM moves across the tape containing symbols but the machine neither reads nor writes. Without #5 the TM is fixed always on the same initial point of the tape and as a consequence does nothing. The functional set TM = {1,2,3,4,5} is IC because its five functions are all necessary just from the beginning. The IC inference is a strong one, in the sense that IC denies evolution in both its guided and unguided sense: simply an IC system has no functioning precursors.
Now let’s pass to the cellular realm. To understand that cell behaves as a TM it is enough to consider one of its TM activities, the RNA transcription process for example. If we consider the transcription of a series of genes the operations sequentially carried out are similar to a transition table. To simplify the description consider the reading of an entire gene as a block instead of the stepwise reading by single nucleotide. Doing so nothing essential changes. The system starts from an initial state and commands the RNA-polymerase to position at the first gene promoter on the DNA strand and read the gene base by base. The related RNA is outputted. RNA-polymerase is directed to move to another position. The inner state changes, other DNA reading and RNA writing steps are carried-out, a new state is reached, and so on. There are of course many other TM cellular processes, even more complex that the RNA synthesis. The following picture shows a two-tape TM (the numbers represent the IC functions according to the above list):
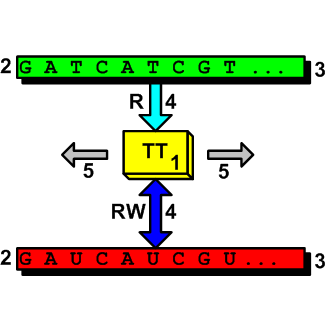
It seems to me that these brief notes should be sufficient to explain that some processes in the cells work as TMs. The ID theory concept of irreducible complexity says us that such cellular TM systems are not generable by evolution. There can be other possible considerations, from different perspectives, that lead us to the same ID inference about TMs/cells. Eventually they will be the subject of other posts in the future.
What I have written in this blog is nothing new, because is implicit in the actual scientific research. In fact many bio-informatics and DNA-computing specialists, since the first ideas and experiments by Leonard Adleman in 1994, acknowledged that cells show TM behaviors and many of them described the TM cellular processing in far more technical detail than me here (about DNA-computing see for example here, here, here).
Unfortunately very few of these scientists (or no one) admit the logical consequence of their researches: whether TMs aren’t products of chance and necessity then cells aren’t too. It is this sort of incoherence that led me to think that such censured truth had to be emphasized here somehow.